You may use this exponential growth calculator to handle exponential growth problems like calculating population increase, compound interest, and doubling time.
<iframe src="https://calculatorhub.org/?cff-form=29" style="width:100%;height:100%;"></iframe>
Ever heard of exponential growth? If not, don’t worry — most people haven’t. While the concept seems complex, it is actually one of the simplest math concepts there is. Exponential growth takes an initial input and multiplies it over time.
To help you understand a bit better, imagine you start out with $1. Now imagine that that amount increases each day by 5 cents. So on Day 2, you’re at $1.05. But because 5 cents is equal to 5%, every 5 days your $1 has compounded into 55 cents. And then again in 60 days you are up to $2.20!
This can be done continuously with any value, and will eventually make that initial starting point grow exponentially by increasing percentage values over time.
Exponential Growth Curve
The amount ‘n’ of yeast cells used to make bread doubles every hour, and the accompanying table shows the facts on how the cells multiply. The graphic below depicts an exponential curve depicting the population’s rise.
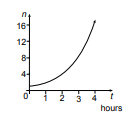
| Time in Hours (t) | 0 | 1 | 2 | 3 | 4 |
| Nos. of Cells (n) | 1 | 2 | 4 | 8 | 16 |
Exponential Growth Calculator Use
- This calculator is easy to use and understand.
- You can calculate exponential growth in real-world scenarios in only three steps.
- The initial value must be entered first.
- The % change in growth rate is entered as the second step.
- The third step is to input the amount of time that has passed.
- The ultimate result in terms of time x(t) will be shown by the calculator.
Formula to Calculate Exponential Growth
The formula to calculate exponential growth is mentioned below:
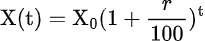
X(t) = exponential growth function
X0 = initial value
r = % growth rate
t = time elapsed
Exponential Growth Examples from Real World
Example 1 : A kind of highly rare deep water fish lives a very long time and has very few children. How many of this species of fish will there be in half a year if there are 625 of them and their growth rate is 1% each month? What will the population look like in 5 years and a 100 years?
Solution :
Population = Initial population × (1 + growth percentage) time period in months . Therefore, in this case:
Population = 625(1 + 2/100)n, where n = number of months.
Case 1 : species in half year
In half year there are 6 months. So in this case the value of ‘n’ will be 6.
Population = 625(1 + 2/100)6
Population = 625(1.02)6
Population = 625(1 + 2/100)6
Population = 625 * 1.1262
Population = 703.8515
Case 2 : species in 5 years
In 5 years there are 60 months. So in this case the value of ‘n’ will be 60.
Population = 625(1 + 2/100)60
Population = 2050.6442427
Case 3 : species in 100 years
In 100 years there are 1200 months. So in this case the value of ‘n’ will be 1200.
Population = 625(1 + 2/100)1200
Population = 1.3064299607e+13
Example 2 : The exponential growth rate of one form of bacteria is 50% every hour. Determine how many bacteria there will be in five hours, three days, and one week if there are 18 bacteria.
Solution :
Population = Initial population × (1 + growth percentage) time period in hours . Therefore, in this case:
Population = 18(1 + 50/100)n, where n = number of hours.
Case 1 : bacteria in 5 hours
Population = 18(1 + 50/100)5
Population = 136.6875
Case 2 : bacteria in 3 days
In 3 days there are 72 hours. So in this case the value of ‘n’ will be 72.
Population = 18(1 + 50/100)72
Population = 8.5870334986e+13
Case 3 : species in 1 week
In 1 week there are 168 hours. So in this case the value of ‘n’ will be 168.
Population = 18(1 + 50/100)168
Population = 1.3064299607e+13