Find the value of any missing side of a right angle triangle using our Pythagorean Theorem Calculator.
<iframe src="https://calculatorhub.org/?cff-form=41" style="width:100%;height:100%;"></iframe>
The Pythagorean theorem is named after Pythagoras, a Greek mathematician who lived around 500 BC. The theorem is a formula that connects the areas of squares that can be drawn on the triangle’s sides for any right-angled triangle.
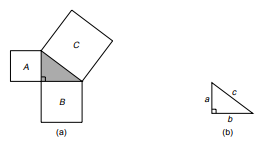
The shaded triangle in fig a is right-angled, and squares A, B, and C are drawn on the triangle’s sides.
Area of square C = area of square A + area of square B
The following is a typical formulation of the theorem:
If the triangle’s sides have lengths of a, b, and c units (see fig b), then
c2 = a2 + b2
In other words, “the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.” Pythagoras’ theorem is used to determine the length of one side of a right-angled triangle when the lengths of the other two sides are known.
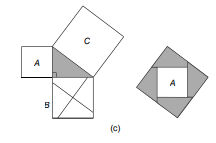
- Fig c allows you to demonstrate the truth of Pythagoras’ theorem in a practical method.
- A copy of the figure and a pair of scissors are required.
- By drawing two lines through the middle of the square, one parallel to the hypotenuse of the triangle, the square B has been divided in half.
- The two lines are perpendicular to each other.
- Remove the three squares from the triangle with scissors. Square B should be cut into four congruent sections.
- Place the four pieces from B, as well as square A, on square C.
- These five pieces should fit together like a jigsaw puzzle to completely cover square C.
- This shows that the area of C equals the sum of the areas of A and B.
Pythagorean Theorem Calculator Use
- This calculator is simple and quick to use.
- From the drop-down list, choose the side of the right-angled triangle to calculate.
- In the relevant input boxes, enter the values for the other two sides.
- The calculator will automatically find the triangle’s unknown side.
Solved Example on Pythagorean Theorem
Example :
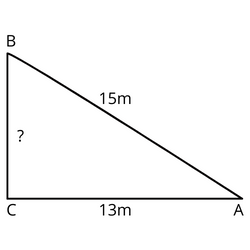
A “flying fox” is created by stretching a wire between two upright poles. The distance between the poles is 13 metres. Find the height of the larger pole if the shorter pole’s height is 6 metres and the wire’s length is 15 metres. Assume the wire is straight and has no “sag.”
Solution :
We need a right-angled triangle to employ Pythagoras’ theorem, which is formed by drawing a horizontal line from the top of the shorter pole to the top of the longer pole. Let x meters be the unknown length of the triangle. This triangle can now be solved using Pythagoras’ theorem.
152 = x2 + 132 Pythagoras’ theorem
225 = x2 + 169
225 – 169 = x2
x2 = 56
x = 7.4833