Poisson Distribution Calculator

The Poisson Distribution Calculator is a free online tool that determines the probability of an event occurring within a specified time range.

<iframe src="https://calculatorhub.org/?cff-form=79" style="width:100%;height:100%;"></iframe>

The Poisson distribution was named after Simeon Devis Poisson, a French mathematician who discovered it. A discrete distribution is the Poisson distribution.

Poisson distribution is mostly used to forecast the probability of an event occurring based on how frequently they have occurred in the past. It estimates the probability of a certain number of occurrences occurring within a specific time frame. It is employed in a variety of real-life scenarios.

Poisson Distribution Calculator Use

• In the first field of the calculator, enter the number of occurrences, and in the second field, provide the rate of success value.
• After you’ve provided all of the required data, the calculator will display the probability value in the third field using the poisson distribution.

Poisson Distribution Formula

The Poisson distribution function can be calculated using the formula:

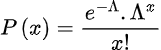
Where,
λ = rate of success.
x = number of occurrences.

Poisson Distribution Solved Examples

We tried to illustrate how to calculate the poisson distribution using some basic examples and solutions.

Example

1. In a juice bar, customers arrive at a rate of 5 per minute on average. Using the Poisson distribution formula, calculate the probability of 12 customers arriving in 1 minute.

Solution :

Given data:

 λ = 5, and x = 12.

By using the above poisson distribution formula,

P(X = x) = (e^-λ. λ^x )/x!
P(X = 12) = (e^-5. 5¹² )/12!
P(X = 12) = 0.003434240285572325.

Multiply the answer by 100 to get the % probability.

The probability of the arrival of 12 customers per minute is 0.34%.

Example

2. If the mean is 5.2, find the mass probability of the function at x = 8.

Solution :

Given data:

 λ = 5.2, and x = 8.

By using the above poisson distribution formula,

P(X = x) = (e^-λ. λ^x )/x!
P(X = 8) = (e^-5.2. 5.2⁸ )/8!
P(X = 8) = 0.07314336219249996

The probability of function is 7.31%.