Whether you’re a student learning BODMAS or just need a quick way to solve tricky expressions, this bodmas calculator has you covered. For now, give this tool a try and let it handle applying BODMAS to solve your expressions correctly!
<iframe src="https://calculatorhub.org/?cff-form=181" style="width:100%;height:100%;"></iframe>
Welcome to our Online BODMAS Calculator! BODMAS rule represents the proper order of operations to follow when solving mathematical expressions. This calculator applies the BODMAS rules to evaluate complex expressions step-by-step. Simply enter your expression and the calculator will solve it in the correct order to give you the right solution. You don’t have to worry about remembering the order yourself – it does the work for you!
How to Use Bodmas Calculator
- Please enter your math expression in the input box and press the calculate.
- The calculator will solve the expression using the BODMAS rule.
- Note that to use the multiplication operator, please use the * (asterisk/star) symbol.
What is BODMAS Rule?
BODMAS is an acronym that denotes the order of operations to follow when evaluating mathematical expressions:
B – Brackets first. Simplify any expressions inside brackets.
O – Orders (Powers and Square Roots). Calculate powers and square roots next, working from left to right.
DM – Division and Multiplication. Perform these operations in order from left to right.
AS – Addition and Subtraction. Perform these operations last in order from left to right.
So in summary:
- Simplify expressions inside brackets first.
- Do powers and square roots from left to right.
- Perform division and multiplication operations from left to right.
- Perform addition and subtraction operations from left to right.
Following this structured order of operations ensures the expression is evaluated correctly. The acronym BODMAS helps us remember the sequence to follow. Applying the BODMAS rule systematically is crucial for accurately solving mathematical and algebraic problems.
How to Solve Math Expression Using Bodmas Rule
Here are 2 examples solving mathematical expressions using the BODMAS rule in a step-by-step tutorial:
Example 1: (2 + 3) * (4 – 2)
Solution :
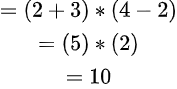
Step 1) Simplify Brackets first:
(2 + 3) = 5
(4 – 2) = 2
Now expression becomes: 5 * 2
Step 2) No Orders (powers/roots):
Step 3) Multiplication:
5* 2 = 10.
Example 2: √64 ÷ 8 + 3
Solution :
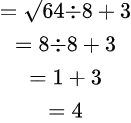
Step 1) There are no brackets.
Step 2) Orders (powers/roots):
√64 = 8
Step 3) Division:
8 ÷ 8 = 1
Step 4) Addition:
1 + 3 = 4
So in summary, always start with simplifying brackets first, then powers/roots, then multiplication/division, and finally addition/subtraction, following the BODMAS rule. This allows you to correctly evaluate any mathematical expression systematically.
Accepted Symbols By Calculator
The accepted symbols for mathematical expressions are standard mathematical operators and symbols. Here are the commonly accepted symbols:
- Addition (+): Use the plus symbol for addition. For example, to add 2 and 3, enter “2 + 3”.
- Subtraction (-): Use the minus symbol for subtraction. For example, to subtract 5 from 8, enter “8 – 5”.
- Multiplication (*): Use the asterisk symbol for multiplication. For example, to multiply 4 by 7, enter “4 * 7”.
- Division (/): Use the forward slash symbol for division. For example, to divide 10 by 2, enter “10 / 2”.
- Exponentiation (^): Use the caret symbol for exponentiation. For example, to calculate 2 raised to the power of 3, enter “2 ^ 3”.
- Parentheses ( and ): Use parentheses to specify the order of operations and to group expressions. For example, “(2 + 3) * (4 – 1)” will calculate the result within the parentheses before performing the multiplication.
- Numbers: You can enter numerical values, both integers and decimals. For example, “2.5” or “3” are valid numerical inputs.
- Implicit Multiplication: The code also handles implicit multiplication when a number is placed next to an opening parenthesis. For example, “2(3 + 4)” will be interpreted as “2 * (3 + 4)”.
These symbols and conventions follow standard mathematical notation and are commonly accepted in mathematical expressions. This tool is designed to correctly evaluate expressions using these symbols and operators.