Using this square root calculator, you can find the square root of any number.
<iframe src="https://calculatorhub.org/?cff-form=52" style="width:100%;height:100%;"></iframe>
The square root is a common operation in mathematics, particularly in the application of Pythagoras’ theorem. We undo the “squaring” action when we take the square root of a number. Taking the square root is referred to as the inverse operation of squaring.
For example, 72 = 49, and the square root of 49 is 7. We generally represent the square root of 49 as √49. It can also be represented in the index form such as 491/2 .
Calculator Use
- To compute the square root of a number, simply input the value in the first field, and the calculator will immediately display the square root value in the second field.
Square Root Formula
The formula to calculate the square root of a number is mentioned below.
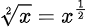
How to Find a Square Root Without Using a Calculator
When you have a scientific calculator on hand, finding a square root of a number is simple. When it comes to manually evaluating, however, the situation is different. Finding the square root can be difficult if you are unfamiliar with some of the foundations of mathematics. But don’t worry, we’ll show you how to find the square root of any number without using a calculator in as simple a manner as possible.
There are various ways to calculate a square root, but we’ve outlined the two that we believe are the most simple from our perspective so that you don’t get confused. The first method is for obtaining the square root of only perfect squares, whereas the second method is for finding the square root of whole numbers (any other number)
1. Finding Square Root of Perfect Squares by Multiplication
To put it differently, the square root of the perfect square is the number multiplied by itself. Don’t be puzzled by the terms we’ve used to illustrate this method; we’re confident that going over the examples will clear up any doubts you may have.
Everyone knows that the square root of 4 is 2, but how do you calculate it? We obtain 4 when we multiply 2 x 2, which is why √4 = 2. That’s what we were attempting to say: the square root of the provided number is the number multiplied by itself to get the value in the question.
Example : Find the square root of 225?
Don’t get panic seeing the big number. Everyone atleast knows tables upto 10. So start multiplying the numbers in mind.
9 x 9 =81 (If this isn’t the square root, you might want to try multiplying a larger number.)
12 x 12 =144 (We’re getting close to the correct answer, so let’s try again.)
15 x 15 = 225 (Yes, the square root of 225 has been discovered.)
Example : Find out square root of 625?
Follow the above given steps until you get the answer.
15 x 15 = 22525 x 25 = 625.
20 x 20 =400
23 x 23 = 529
2. Finding the Square Root of Other Numbers
It’s a lot more difficult to find the square root of other numbers than it is to find the square root of perfect squares. You’ll need a little more time than the above method to find the square root. Additionally, this method requires you to work with decimals. This strategy, however, has no alternatives. However, you may use our square root calculator to calculate the square root of any number.
This method is all about guess. For example, lets say you want to find out the square root of 8. You know that 9 is the perfect square with its square root 3 (3 x 3 = 9) and the square root of 4 is 2 (2 x 2 = 4). So logically the square root of 8 must lie in between 2 and 3.
So let’s start multiplying the numbers between them one by one till we arrive at the answer. However, because we are dealing with decimals, we may need to round off the answer if we cannot get an exact figure.
1st guess is 2.5 (always select the middle value between 2 numbers). So multiplying 2.5 x 2.5 we get 6.25.
2nd guess is 2.7, 2.7 x 2.7 = 7.29.
3rd guess is 2.8, 2.8 x 2.8 = 7.84.
4th guess is 2.9, 2.9 x 2.9 = 8.41.
As you can see, we have two numbers: 7.84 (square of 2.8) and 8.41. (square of 2.9). This demonstrates that the square root of 8 is exactly between 2.8 and 2.9. So, let’s keep going with the above procedure.
1st guess is 2.85, 2.85 x 2.85 = 8.1225
2nd guess is 2.82. 2.82 x 2.82 = 7.9524
3rd guess is 2.83, 2.83 x 2.83 = 8.0089 ≈ 8 (Yes, we have finally found out the square root of 8.)