Have a challenge performing long subtractions? Do not worry; we have got you covered. This long subtraction calculator is capable of quickly calculating the difference of long numbers, even those containing decimals.
<iframe src="https://calculatorhub.org/?cff-form=119" style="width:100%;height:100%;"></iframe>
What is Long Subtraction?
Long subtraction is the same as ordinary subtraction. The same procedure is used, but with large, complex numbers that may include decimal numbers. This process is also known as “column subtraction”.
Because the numbers are arranged in columns for the subtraction, the process is called column subtraction. As shown in the image below.

We’ve provided solved examples for various types of numbers below, so you can understand the process of long subtraction and perform the calculations on your own. We made every effort to keep the tutorial as simple as possible.
Long Subtraction Calculator Use
- It’s really easy to use this long subtraction calculator.
- You only need to enter the numbers separated by comma (,) to find the difference between the numbers (for ex: 9535, 859, 1595, 20.5 etc.)
- You can even input decimal numbers and there is no limit for the entering the numbers.
- The ultimate result of the lengthy subtraction of all the numbers will be shown by the calculator in no time.
Long Subtraction Examples
We have described the long subtraction process step by step. Using this method, we have resolved a number of examples.
Example :
1. Carry out the long subtraction of : 2155-1521.
Solution :
This is a very simple process, and we will walk you through it step by step.
Step 1 : Arrange the numbers in a column, one beneath the other. Draw a horizontal line across the top of the column and two horizontal lines (with little space in between) across the bottom of the column after you’ve compiled both the numbers.
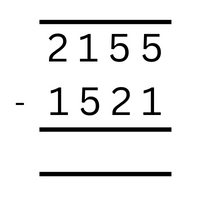
Step 2 : Now that you’ve compiled all of the numbers, perform the subtraction of numbers in the first column from the right side. (5-1 = 4).

Step 3 : After subtracting, (5 – 1 = 4) we get the answer as 4. Now write down the digit 4 in the bottom of the same column.

Step 4 : Now proceed to the second column from the right side. We have two numbers to perform the subtraction. Subtracting 2 from 5, we get, 3. Write down the digit 3 at the bottom of the same column.

Step 5 : Now in the third column the digit in the first row (1) is smaller than the digit in the second row (5). Here we have to borrow the value from the neighboring column that is fourth column. In the forth column, the value at the top row is 2, so we can borrow one digit and give it to the digit in the first row of third column.
The digit 2 in the first row of fourth column becomes 1 after giving its one digit to the third column and the digit 1 in first row the third column becomes 11. Here we will not add the borrowed value. Just place the borrowed value before the number.
So, 11-5 = 6. Write down the value at the bottom of the third column.

Step 6 : In the forth column we have both the digits common i.e. 1, so subtracting 1 from 1 we get 0. So the final answer is 634.
Long Subtraction : 2155-1521 = 634.
Example : (Long Subtraction with Decimals)
2. Carry out the long subtraction of : 18.75 – 9.81
Solution :
In this example, we must deal with decimals. But it’s not a big deal. All of the steps discussed in the first example apply here and to all long-subtraction problems.
When arranging the numbers in the column format, make sure that the decimal of each number is one beneath the other, regardless of how many numbers are after or before the decimal point.
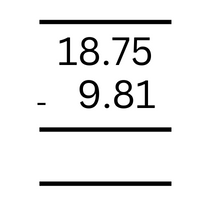
Step 1 : Perform the subtraction for first column form the right side. We get, 5-1 = 4. Write down at the bottom of the same column.

Step 2 : Perform the subtraction for second column form the right side. Her top row digit (7) is smaller than bottom row digit (8), so we have to borrow a digit form the next column (third column). In the third column we have number 8 at the top row so we can borrow a digit and give it to number 7 to become 17.
Now that 7 has became 17 after borrowing a digit from 8, we can perform the subtraction.
We get, 17-8 = 9. Write down 9 at the bottom of the same second column.

Step 3 : In third column 8 has became 7 after giving a digit to 7. Here we have to borrow one more time as the top row value (7) is smaller than bottom row value (9).
In the fourth column we have digit 1 at the top row so we have to borrow the digit from the top row of fourth column. After borrowing a digit, 7 becomes 17 and 1 becomes 0.
After subtracting (17-9 = 8), We get 8 as the answer. Write down 8 at the bottom of the column.
So the final answer is 8.94, as there is no value left in the fourth column.

Long Subtraction : 18.75-9.81 = 8.94