Average deviation calculator can easily calculate the average deviation of any given data set. It can also find the mean value and count the data set observations.
<iframe src="https://calculatorhub.org/?cff-form=122" style="width:100%;height:100%;"></iframe>
What is Average Deviation?
Average deviation is a statistical tool that computes the mean of various variations in a data set. By measuring how far a deviation is from the mean or median of the data set, we can determine average deviation.
You can easily calculate the average deviation value for a small set of data manually, but if you want to find the average deviation value for a large set of data, you will need to use some illustration calculator tools.
Average Deviation Calculator Use
- In the first field, enter the values from the data set. Make sure to comma-separate each value.
- It will show the average deviation of the entered data set as well as calculate the mean value.
Average Deviation Formula
Average deviation for any data set can be found using the formula mentioned below.
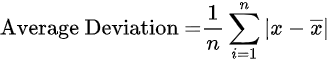
Where,
n = total number of data values.
x = individual values in given data set.
x̄ = mean value.
Examples on Finding Average Deviation
The formula given above can be used to get the dataset’s average deviation. Below, we’ve tried to explain a few examples that will help you understand how the formula functions.
Example :
1. Using the average deviation formula, calculate the average deviation of the following data: 8, 16, 32, 64, 128.
Solution :
We have given dataset value (x) = 8, 16, 32, 64, 128.
Total number of values (n) = 5.
We can now find the mean value of the data set. To find the mean just divide the sum of all observations by the total number of observations.
Mean (x̄) = (8+16+32+64+128) / n
Mean (x̄) = (8+16+32+64+128) / 5
Mean (x̄) = 248 / 5
Mean (x̄) = 49.6
we have also created a arithmetic mean calculator which quickly calculates the mean value of large data values.
Using the average deviation formula,
Average deviation = (1/n)Σ |x – x̅|
Average deviation = ( |8-49.6| + |16-49.6| + |32-49.6| + |64-49.6| + |128-49.6| ) / 5
Average deviation = ( |-41.6| + |-33.6| + |-17.6| + |14.4| + |78.4| ) / 5
Average deviation = (41.6 + 33.6 + 17.6 + 14.4 + 78.4) / 5
Average deviation = 185.6 / 5
Average deviation = 37.12
Average Deviation of the dataset 8, 16, 32, 64, 128 is 37.12.
Example :
2. This season, a hockey player has played in seven games. Each game’s scoring figures are 4, 9, 12, 1, 3, 1, and 5. Calculate the mean and the average deviation.
Solution :
We have given dataset value in the form of each game’s scoring figures (x) = 4, 9, 12, 1, 3, 1, 5.
Total number of values (n) = 7.
We can now find the mean value of the data set. To find the mean just divide the sum of all observations by the total number of observations.
Mean (x̄) = (4+9+12+1+3+1+5) / n
Mean (x̄) = (4+9+12+1+3+1+5) / 7
Mean (x̄) = 35 / 7
Mean (x̄) = 5
Using the average deviation formula,
Average deviation = (1/n)Σ |x – x̅|
Average deviation = ( |4-5| + |9-5| + |12-5| + |1-5| + |3-5| + |1-5| + |5-5| ) / n
Average deviation = ( |-1| + |4| + |7| + |-4| + |-2| + |-4| + |0| ) / 7
Average deviation = (1 + 4 + 7 + 4 + 2 + 4 + 0) / 7
Average deviation = 22 / 7
Average deviation = 3.143
Average Deviation of the dataset 4, 9, 12, 1, 3, 1, 5 is 3.143.
Mean Value of the dataset 4, 9, 12, 1, 3, 1, 5 is 5.