The subtraction of two exponents can be done quickly with this online subtracting exponents calculator. Additionally, you can also subtract numbers with negative exponents.
<iframe src="https://calculatorhub.org/?cff-form=118" style="width:100%;height:100%;"></iframe>
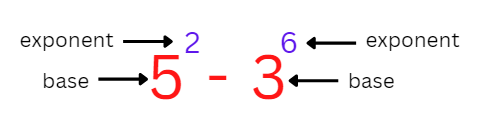
What is an Exponent?
It is easier to express a number or an expression in exponent form when it is multiplied by itself numerous times. 125, for example, is written as 53 and equals (5 * 5 * 5).
The exponent form of (5 * 5 * 5) is called 53, and its value is 125. When 53 replaces 125, we say the base is 5 and the exponent is 3. Exponent is also known as index. Indices is the plural form of index.
The number of times the base is multiplied by itself is the power. In Example 53, we state that 125 is the third power of 5, or that 125 is 5 to the power of 3 (53).
How to Use Subtracting Exponents Calculator?
- This calculator for subtracting exponents can subtract one exponent from another within seconds.
- Enter the exponents and base values in the appropriate fields to subtract the exponents in the above calculator.
- The calculator will instantly find the difference between both the exponents.
- If you have a negative exponents value, simply add the minus(-) sign before entering the value.
How to Subtract Exponents ?
Subtraction of exponents is very similar to the addition of exponents, which we have covered in a recent article. Exponents must be simplified before they can be subtracted, and the values obtained after the simplification are then subtracted. We have answered a few examples below that should put all of your questions about the subtraction of exponents to rest.
Case 1 : Different Base & Exponents
Example
1. Subtract exponents : 35 – 43
Solution :
First exponent : 35 = 3 x 3 x 3 x 3 x 3 = 243. (multiplying the base value{3}, number of times of exponent value {5})
Second exponent : 43 = 4 x 4 x 4 = 64. (multiplying the base value {4}, number of times of exponent value {3})
We have simplified both the exponents, now just perform the subtraction.
= 56 – 43
= (3 x 3 x 3 x 3 x 3) – (4 x 4 x 4)
= 243 – 64
= 179.
The subtraction of exponents 35 + 43 = 179.
Example
2. Subtract exponents : 36 – 24
Solution :
We’ll follow the same procedure as in the previous example.
= 36 – 24
= (3 x 3 x 3 x 3 x 3 x 3) – (2 x 2 x 2 x 2)
= 729 – 16
= 713
The subtraction of exponents 36 – 24 = 713.
Case 2 : Same Base & Exponents
Example
3. Subtract exponents : 53 – 53
Solution :
When the base and exponents are the same, you can use the same above process as in case 1 to solve the problem.
= 53 – 53
= (5 x 5 x 5) – (5 x 5 x 5)
= 125 – 125
= 0
The subtraction of exponents 53 – 53 = 0.
Case 3 : Negative Exponents
Example
4. Subtract exponents : 8-3 – 5-4
Solution :
The exponents in this case are negative (-). The approach of addressing the problem is the same as it was in case 1 even if the exponents signs are negative since the base and exponents values differ.
But before moving on, be aware that the method of simplification could change slightly. As the exponents have a negative sign, we must first change it to a positive sign (+) in order to move forward. A step-by-step process for performing the addition of negative exponents is shown below.
First Exponent = 8-3, We must divide the entire term by 1 in order to make this exponent positive.
First Exponent = 8-3 = 1/83, Once we have changed the exponent’s value to positive, simply simplify as usual.
First Exponent = 8-3 = 1/83 = 1/ (8 x 8 x 8) = 1/ 512 = 0.001953125
Second Exponent = 5-4 = 1/54 = 1/ (5 x 5 x 5 x 5) = 1/ 625 = 0.0016
= 8-3 – 5-4
= 1/83 – 1/54
= 0.001953125 – 0.0016
= 0.000353125
The subtraction of exponents 8-3 – 5-4 = 0.000353125
Example
5. Subtracting exponents : 83 – 6-4
Solution :
Now here the first exponent isn’t negative so we can simplify it with normal process.
First exponent = 83 = 8 x 8 x 8 = 512.
Convert the second exponent into positive form by dividing it by 1 and simplifying.
Second exponent = 6-4 = 1/64 = 1/(6 x 6 x 6 x 6) = 1/1296 = 0.00077160493
= 83 – 6-4
= 512 – 0.00077160493
= 511.99
The subtraction of exponents 83 – 6-4 = 511.99