Volume of Torus Calculator

Have you ever tried to figure out how big a tire tube or donut is? If that’s the case, then this torus volume calculator is made just for you. You can quickly calculate the volume of torus-shaped objects with this calculator.

<iframe src="https://calculatorhub.org/?cff-form=94" style="width:100%;height:100%;"></iframe>

The torus is a doughnut-shaped three-dimensional figure that is generated when a circle is spun around a line in its plane but not through its axis.

To put it simply, a torus is a three-dimensional form created by rotating a tiny circle along a line drawn by a larger circle.

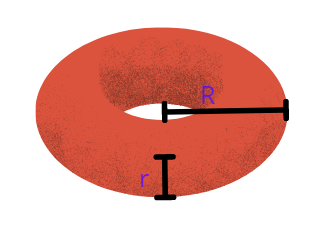
A tire’s inner tube is the most common example of a torus. Consider a circle on a plane with a diameter that is perpendicular to the straight line. The resulting figure is a torus, which is a hollow round tube.

In the above torus figure, ‘r’ represents the minor radius and ‘R’ represents the major radius.

Volume of Torus Calculator Use

• To get the volume of a torus, you must first determine the inner (r) and outer (R) radii of the torus.
• In the above calculator, enter the two radius values in the appropriate fields.
• The calculator will calculate the torus volume.

Torus Volume Formula

A simple formula can be used to calculate the volume of a torus. Using the formula below, you can calculate the volume of a torus using the inner and outer radius.

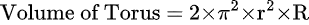
How to Find the Volume of a Torus

The shape of the torus may lead one to believe that manually calculating the volume of the torus is impossible. But that’s not the case. Simply measuring the radius of the inner and outer circle yields the volume. To calculate the volume of a torus, use the torus volume formula shown above.

We will demonstrate how to compute the volume of torus shape using solved examples.

Example

1. The outer radius of a ring-shaped object is 22 cm, whereas the inner radius is 12 cm. Calculate the torus volume for that object.

Solution :

Outer radius (R) = 22 cm
Inner radius (r) = 12 cm

Using the torus volume formula,

Volume = 2 x π² x r² x R
Volume = 2 x 3.141592654² x 12² x 22
Volume = 62533.8135 cu.cm

The volume of ring-shaped object is 62533.8135 cubic centimeters.

Example

2. Tire tubes have a 2 ft outer radius and a 0.5 ft inner radius. Determine the tube’s volume.

Solution :

Outer radius (R) = 2 ft
Inner radius (r) = 0.5 ft

Using the torus volume formula,

Volume = 2 x π² x r² x R
Volume = 2 x 3.141592654² x 0.5² x 2
Volume = 9.8696044 cu.ft

The volume of tyre tube is 9.8696044 cubic feet.