You can simply calculate the volume of any triangular pyramid using this triangle pyramid calculator.
<iframe src="https://calculatorhub.org/?cff-form=95" style="width:100%;height:100%;"></iframe>
A triangular pyramid is a geometric solid with a triangular base and triangles having a common vertex on all three lateral faces. Triangular pyramids can be regular, irregular, or right-angled.
A triangular pyramid is made up of three primary parts. The first is the base, which is, of course, a triangle. The faces are made up of three triangles. The apex is the point at the top of the pyramid where all of the faces meet.
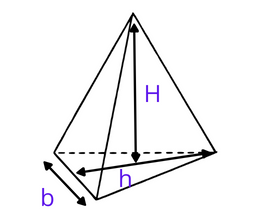
In the above triangular pyramid figure, ‘b’ represents the base, ‘h’ represents the base height and the ‘H’ represents the height of the pyramid.
Volume of Triangular Pyramid Calculator Use
- Calculating the volume using this triangular pyramid calculator is simple.
- From the dropdown list, choose whether you know the triangular pyramid’s base area and height or its side length.
- Enter the base area and height, or the side length, of a triangular pyramid.
- The volume will be displayed by the calculator based on the entered inputs.
Triangular Pyramid Volume Formula
A simple formula can be used to calculate the volume of a triangular pyramid. Using the formula below, you can calculate the volume of a triangular pyramid using the base area and the height of the triangular pyramid.
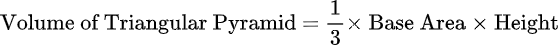
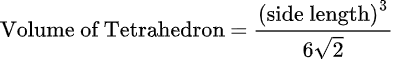
How to Find the Volume of Triangular Pyramid
Finding the volume of a triangular pyramid may appear tough, but it is less difficult than gazing at the pyramid’s top from the bottom. The volume of a triangular pyramid can be calculated using the formula stated above. You simply need to determine the triangular pyramid’s base area and height.
Some of you may be wondering how to calculate the triangle’s base area.
For those who are unsure, we can tell you that the base area of the triangle can be calculated using the area formula (1/2 x b x h) that we learned in school.
We’ve included some solved examples below to help you tackle the triangle pyramid volume problems quickly.
Example
1. find the volume of the triangular pyramid below.
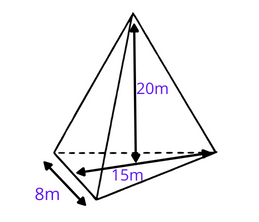
Solution :
Height of triangular pyramid (H) = 20 m
Base height (h) = 15 m
Base (b) = 8 m
First we shall find the base area of the triangular pyramid.
Base Area = 1/2 x b x h
Base Area = 1/2 x 8 x 15
Base Area = 60 m2
Using the triangular pyramid volume formula,
Volume = 1/3 x base area x height
Volume = 1/3 x 60 x 20
Volume = 399.999996 m3
The volume of a triangular pyramid is 399.999996 cubic meters.
Example
2. Calculate the volume of a tetrahedron having sides that are 4.5 feet long.
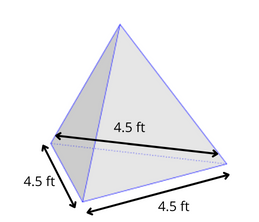
Solution :
side length = 4.5 ft
You’re probably wondering what a tetrahedron is.
When the triangular pyramid has all its triangular faces equilateral is called as regular tetrahedron. In this problem we know that all the base sides of the triangular pyramid is 4.5 feet.
Using the tetrahedron volume formula,
Volume = (side length)3 / 6√2
Volume = (4.5)3 / 8.485
Volume = 91.125 / 8.485
Volume = 10.7395404 cu.ft
The volume of tetrahedron is 10.7395404 cubic feet.