If you’re looking for a web tool to help you determine the central angle of circle, you’ve come to the right place. Simply enter the radius and arc length into this central angle calculator to determine the circle’s central angle.
<iframe src="https://calculatorhub.org/?cff-form=88" style="width:100%;height:100%;"></iframe>
When angles or polygons are drawn inside circles, a central angle is any angle whose vertex is at the circle’s center point. The radii of the circle are the sides of a central angle.
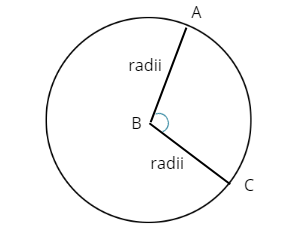
In the above figure, the distance between point A to Point C is called as the arc length. It is defined as the section of a circle defined by two or more points.
Central Angle Calculator Use
- This central angle calculator online is very simple to use.
- All you have to do is fill in the required fields with the arc length and radius of the circle.
- The diameter of the circle and the central angle will be displayed by the calculator based on the given data.
- From the dropdown menu, you can convert the central angle from degrees to radians and radians to degrees.
Central Angles Formula
Using the formula below, you can quickly find the central angle of any given circle.
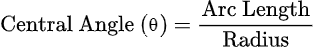
How to Calculate the Central Angle
Calculating the circle’s central angle is a simple task. You can easily compute the central angle if the vertex of the angle is at the centre of the circle; all you need is the radius of the circle, which is one arm of the angle, and the arc length.
The central angle is calculated by dividing the arc length by the radius of circle. To clear up any doubts, we’ve included several solved examples below.
Example
1. Find the central angle of the circle below.
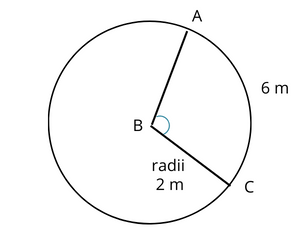
Solution :
Radius of circle = 2m
Arc length (AC) = 6m
Using the central angle formula,
Central Angle = Arc Length/ Radius
Central Angle = 6/ 2
Central Angle = 3 rad.
You can quickly convert the unit of the angle to degrees by using our radians to degrees calculator. If you want to manually convert the angle unit, follow the steps below.
To convert the angle unit from radians to degrees, just multiply the value by (180/π).
Simply multiply the angle value by (180/π) to convert the angle unit from radian to degrees.
Central Angle = 3 x (180/π)
Central Angle = 3 x (180/3.14)
Central Angle = 3 x 57.325
Central Angle = 171.9°
The central angle ABC is 3 rad or 171.9°.
Example
2. Find the central angle, where the arc length measurement is about 32 cm and the length of the radius measures 17 cm.
Solution :
arc length = 32 cm
radius = 17 cm
Using the central angle formula,
Central Angle = Arc Length/ Radius
Central Angle = 32/ 17
Central Angle = 1.8824 radian
The central angle unit must now be converted from radians to degrees. You can do so by using our online radians to degrees converter or by following the steps outlined below to convert the angle from one unit to another.
Central Angle = 1.8824 x (180/π)
Central Angle = 1.8824 x (180/3.14)
Central Angle = 1.8824 x 57.325
Central Angle = 107.9°
The central angle is 1.8824 rad or 107.9°.
Example
3. Determine the radius of a circle whose central angle is 69.48° and the length of the arc formed is 14 cm.
Solution :
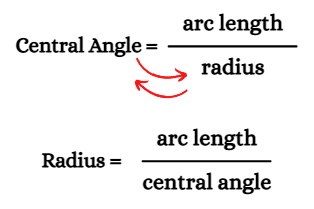
The central angle (69.48°) and arc length (14 cm) are already given in this problem. We must determine the radius of the circle. In this case, the central angle formula must be modified.
The image below shows how to modify the central angle formula to obtain the radius of a circle.
However, before we can use the modified formula, we must first convert the central angle unit from degrees to radians. We’ll do it this way because the original central angle formula yields the final result in radians. As a result, we will also use the central angle in radians unit.
You can use our online degrees to radians converter or the steps below to convert the central angle from degrees to radians.
To convert an angle from degrees to radians, just multiply the angle value by (π/180).
Central Angle = 69.48° x (π/180)
Central Angle = 69.48 x (3.14/180)
Central Angle = 69.48 x 0.0174
Central Angle = 1.21204 radian
Using the modified formula,
Radius = arc length / central angle
Radius = 14 / 1.21204
Radius = 11.55 cm
The radius of the circle is 11.55 cm