You may quickly obtain the acute angle that corresponds to the angle entered in this reference angle calculator.
<iframe src="https://calculatorhub.org/?cff-form=87" style="width:100%;height:100%;"></iframe>
The reference angle is the angle formed by the terminal side and the x-axis positioned between them. It’s the smallest angle that the provided angle’s terminal side can make with the x-axis. It must be less than 90 degrees and constantly positive.
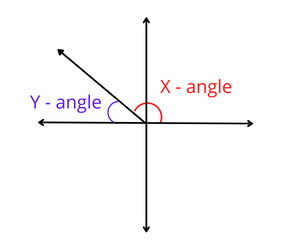
The concept of reference angle can be understood from the diagram above. The reference angle of the X-angle is the Y-angle.
Reference Angle Calculator Use
- This online calculator is really easy to use.
- You can enter the angle value in the first field to find the reference angle of your desired angle.
- The calculator will then display the reference angle of the entered angle value when you press the calculate button.
- By clicking the reset button, you can erase the old data and calculate the reference angle for another angle value.
Reference Angle Formula
Depending on whether your initial angle is in the first, second, third, or fourth quadrant, there are four formulas to calculate the reference angle.
If the initial angle is between 0° and 90° (first quadrant), use the formula below.
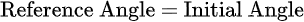
If the initial angle is between 90° and 180° (second quadrant), use the formula below.
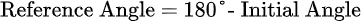
If the initial angle is between 180° and 270° (third quadrant), use the formula below.
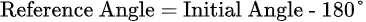
If the initial angle is between 270° and 360° (fourth quadrant), use the formula below.
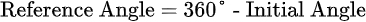
What if theta value is greater than 360 degrees? Don’t be perplexed; we’re always available to answer your questions.
If the initial angle value is more than 360°, compute the coterminal angle by subtracting 360° until θ is between 0° and 360°. Once you have a θ value that is less than or equal to 360°, you can apply from above four formulas to calculate the reference angle.
How to Calculate the Reference Angle
You can simply find the reference angle of any angle using the formula above. We’ve solved a few examples to help you grasp the concept of determining the reference angle.
Example
1. Find the reference angle for 108°.
Solution :
From the given problem, we can determine that 108° lies in the second quadrant. Use the above mentioned reference angle formula for angles between 90° – 180° (second quadrant).
Using formula,
Reference Angle = 180° – Initial Angle
Reference Angle = 180° – 108°
Reference Angle = 72°
The reference angle of 108° is 72°
2. Find the reference angle for 240°.
Solution :
From the given problem, we can determine that 240° lies in the third quadrant. Use the above mentioned reference angle formula for angles between 180°-270° (third quadrant).
Using formula,
Reference Angle = Initial Angle – 180°
Reference Angle = 240°– 180°
Reference Angle = 60°
The reference angle of 240° is 60°
3. Find the reference angle for 540°.
Solution :
Because the initial angle in this problem is greater than 360°, we must subtract 360° from it until the initial angle is less than or equal to 360°.
Initial angle = 540° – 360° = 180°
We get 180° after subtracting the initial angle by 360°, which is less than 360°, therefore we may continue to get the reference angle. Both formulas can be used because 180° is the middle line of the second and third quadrants.
Using formulas,
By second quadrant formula,
Reference Angle = 180° – Initial Angle
Reference Angle = 180° – 180°
Reference Angle = 0°
By third quadrant formula,
Reference Angle = Initial Angle – 180°
Reference Angle = 180° – 180°
Reference Angle = 0°
The reference angle of 540° is 0°
4. Find the reference angle for 1089°.
Solution :
Because the initial angle in this problem is greater than 360°, we must subtract 360° from it until the initial angle is less than or equal to 360°.
Initial angle = 1089° – 360° = 729°
Initial angle = 729° – 360° = 369°
Initial angle = 369° – 360° = 9°
We get 9° after subtracting the initial angle three times by 360°, which is less than 360°, therefore we may continue to get the reference angle. As the initial angle 9° lies in the first quadrant so we may use the first quadrant formula to find the reference angle.
Using formula,
Reference Angle = Initial Angle
Reference Angle = 9°
Reference Angle = 9°
The reference angle of 1089° is 9°
Note: You may always use the calculator above to double-check your answers.
Reference Angle of Negative Angle
We’ve already learnt how to find the reference angle of a positive angle. But what if you have to calculate the reference angle of a negative angle? Don’t merely scroll up to view the formulas because we haven’t included any negative angle formulas and they don’t exist.
The process of determining the reference angle for negative angles is identical to that of determining the reference angle for positive angles. We’ll show you how to find the reference angle of negative angles in the simplest way possible. We’ll use a basic example to explain this.
1. Find the reference angle of -225°.
Solution :
As you can see, the initial angle is negative, and we must determine its reference angle. To find the reference angle of a negative number, one simple method is to consider it as a positive number (i.e., find its absolute value).
Once you’ve converted the negative angle to a positive angle, the rest of the steps are the same as they are for determining the positive angle’s reference angle.
Initial Angle = -225°
Absolute Value of -225° = 225°
From the given problem, we can determine that 225° lies in the third quadrant. Use the above mentioned reference angle formula for angles between 180° – 270° (third quadrant).
Using formula,
Reference Angle = Initial Angle – 180°
Reference Angle = 225° – 180°
Reference Angle = 45°
The reference angle of -225° is 45°
Reference Angle of 1°-360°
The reference angle of 1° to 90° equals the initial angle. For example, a reference angle of 1° is 1°, 8° is 8°, a reference angle of 55° is 55°, and so on up to 90°. The reference angles of 91° – 360° are listed in the table below.
| Reference Angle of | |
| 91° | 89° |
| 92° | 88° |
| 93° | 87° |
| 94° | 86° |
| 95° | 85° |
| 96° | 84° |
| 97° | 83° |
| 98° | 82° |
| 99° | 81° |
| 100° | 80° |
| 101° | 79° |
| 102° | 78° |
| 103° | 77° |
| 104° | 76° |
| 105° | 75° |
| 106° | 74° |
| 107° | 73° |
| 108° | 72° |
| 109° | 71° |
| 110° | 70° |
| 111° | 69° |
| 112° | 68° |
| 113° | 67° |
| 114° | 66° |
| 115° | 65° |
| 116° | 64° |
| 117° | 63° |
| 118° | 62° |
| 119° | 61° |
| 120° | 60° |
| 121° | 59° |
| 122° | 58° |
| 123° | 57° |
| 124° | 56° |
| 125° | 55° |
| 126° | 54° |
| 127° | 53° |
| 128° | 52° |
| 129° | 51° |
| 130° | 50° |
| 131° | 49° |
| 132° | 48° |
| 133° | 47° |
| 134° | 46° |
| 135° | 45° |
| 136° | 44° |
| 137° | 43° |
| 138° | 42° |
| 139° | 41° |
| 140° | 40° |
| 141° | 39° |
| 142° | 38° |
| 143° | 37° |
| 144° | 36° |
| 145° | 35° |
| 146° | 34° |
| 147° | 33° |
| 148° | 32° |
| 149° | 31° |
| 150° | 30° |
| 151° | 29° |
| 152° | 28° |
| 153° | 27° |
| 154° | 26° |
| 155° | 25° |
| 156° | 24° |
| 157° | 23° |
| 158° | 22° |
| 159° | 21° |
| 160° | 20° |
| 161° | 19° |
| 162° | 18° |
| 163° | 17° |
| 164° | 16° |
| 165° | 15° |
| 166° | 14° |
| 167° | 13° |
| 168° | 12° |
| 169° | 11° |
| 170° | 10° |
| 171° | 9° |
| 172° | 8° |
| 173° | 7° |
| 174° | 6° |
| 175° | 5° |
| 176° | 4° |
| 177° | 3° |
| 178° | 2° |
| 179° | 1° |
| 180° | 0° |
| 181° | 1° |
| 182° | 2° |
| 183° | 3° |
| 184° | 4° |
| 185° | 5° |
| 186° | 6° |
| 187° | 7° |
| 188° | 8° |
| 189° | 9° |
| 190° | 10° |
| 191° | 11° |
| 192° | 12° |
| 193° | 13° |
| 194° | 14° |
| 195° | 15° |
| 196° | 16° |
| 197° | 17° |
| 198° | 18° |
| 199° | 19° |
| 200° | 20° |
| 201° | 21° |
| 202° | 22° |
| 203° | 23° |
| 204° | 24° |
| 205° | 25° |
| 206° | 26° |
| 207° | 27° |
| 208° | 28° |
| 209° | 29° |
| 210° | 30° |
| 211° | 31° |
| 212° | 32° |
| 213° | 33° |
| 214° | 34° |
| 215° | 35° |
| 216° | 36° |
| 217° | 37° |
| 218° | 38° |
| 219° | 39° |
| 220° | 40° |
| 221° | 41° |
| 222° | 42° |
| 223° | 43° |
| 224° | 44° |
| 225° | 45° |
| Reference Angle of | |
| 226° | 46° |
| 227° | 47° |
| 228° | 48° |
| 229° | 49° |
| 230° | 50° |
| 231° | 51° |
| 232° | 52° |
| 233° | 53° |
| 234° | 54° |
| 235° | 55° |
| 236° | 56° |
| 237° | 57° |
| 238° | 58° |
| 239° | 59° |
| 240° | 60° |
| 241° | 61° |
| 242° | 62° |
| 243° | 63° |
| 244° | 64° |
| 245° | 65° |
| 246° | 66° |
| 247° | 67° |
| 248° | 68° |
| 249° | 69° |
| 250° | 70° |
| 251° | 71° |
| 252° | 72° |
| 253° | 73° |
| 254° | 74° |
| 255° | 75° |
| 256° | 76° |
| 257° | 77° |
| 258° | 78° |
| 259° | 79° |
| 260° | 80° |
| 261° | 81° |
| 262° | 82° |
| 263° | 83° |
| 264° | 84° |
| 265° | 85° |
| 266° | 86° |
| 267° | 87° |
| 268° | 88° |
| 269° | 89° |
| 270° | 90° |
| 271° | 89° |
| 272° | 88° |
| 273° | 87° |
| 274° | 86° |
| 275° | 85° |
| 276° | 84° |
| 277° | 83° |
| 278° | 82° |
| 279° | 81° |
| 280° | 80° |
| 281° | 79° |
| 282° | 78° |
| 283° | 77° |
| 284° | 76° |
| 285° | 75° |
| 286° | 74° |
| 287° | 73° |
| 288° | 72° |
| 289° | 71° |
| 290° | 70° |
| 291° | 69° |
| 292° | 68° |
| 293° | 67° |
| 294° | 66° |
| 295° | 65° |
| 296° | 64° |
| 297° | 63° |
| 298° | 62° |
| 299° | 61° |
| 300° | 60° |
| 301° | 59° |
| 302° | 58° |
| 303° | 57° |
| 304° | 56° |
| 305° | 55° |
| 306° | 54° |
| 307° | 53° |
| 308° | 52° |
| 309° | 51° |
| 310° | 50° |
| 311° | 49° |
| 312° | 48° |
| 313° | 47° |
| 314° | 46° |
| 315° | 45° |
| 316° | 44° |
| 317° | 43° |
| 318° | 42° |
| 319° | 41° |
| 320° | 40° |
| 321° | 39° |
| 322° | 38° |
| 323° | 37° |
| 324° | 36° |
| 325° | 35° |
| 326° | 34° |
| 327° | 33° |
| 328° | 32° |
| 329° | 31° |
| 330° | 30° |
| 331° | 29° |
| 332° | 28° |
| 333° | 27° |
| 334° | 26° |
| 335° | 25° |
| 336° | 24° |
| 337° | 23° |
| 338° | 22° |
| 339° | 21° |
| 340° | 20° |
| 341° | 19° |
| 342° | 18° |
| 343° | 17° |
| 344° | 16° |
| 345° | 15° |
| 346° | 14° |
| 347° | 13° |
| 348° | 12° |
| 349° | 11° |
| 350° | 10° |
| 351° | 9° |
| 352° | 8° |
| 353° | 7° |
| 354° | 6° |
| 355° | 5° |
| 356° | 4° |
| 357° | 3° |
| 358° | 2° |
| 359° | 1° |
| 360° | 0° |