This complementary angles calculator can determine the complementary angle of your desired angle.
<iframe src="https://calculatorhub.org/?cff-form=85" style="width:100%;height:100%;"></iframe>
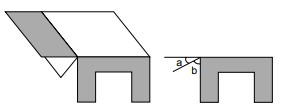
If two angles add up to produce a 90-degree angle, they are complementary. Figure a depicts a drop-leaf table with the leaf in a horizontal position at first. The leaf then swings around the table’s edge through angle a, then through angle b, until it is vertical. Because the two angles a and b sum up to 90°, they are complementary angles. As a result, a + b = 90°. Angle a is said to be the complement of angle b, and vice versa.
Complementary Angles Calculator Use
- This online calculator is really easy to use.
- You can enter the angle value in the first field to find the complementary angle of your desired angle.
- The calculator will then display the complementary angle of the entered angle value when you press the calculate button.
- By clicking the reset button, you can erase the old data and calculate the complementary angle for another angle value.
Complementary Angles Formula
Using the formula below, you can quickly find the complementary angle of any given angle.
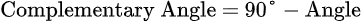
Types of Complementary Angles
The complementary angle is primarily divided into two types:
- Adjacent Complementary Angles
- Non-adjacent Complementary Angles
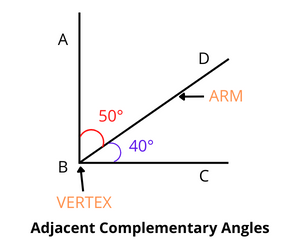
Adjacent Complementary Angles : When a right angle is divided into two halves, we get two angles with the same vertex and arm. Angles of this type are known as adjacent complementing angles. The sum of two adjacent complementary angles is always 90 degrees. The diagram above can assist you in comprehending the idea of adjacent complementary angles.
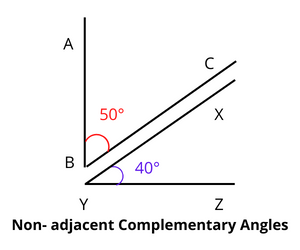
Non-adjacent Complementary Angles : Non-adjacent complementary angles are formed when two angles are not adjacent, that is, when they do not share the same vertex and common arm. This form of angle, like the adjacent complementary angles, sums up to 90 degrees. The illustration above can assist you in comprehending the concept of non-adjacent complementary angles.
How to Find Complementary Angles
We’ve seen that two complimentary angles add up to 90 degrees (i.e., x + y = 90°). Finding the complementary angle is not difficult at all. To find it, simply subtract the angle value from 90°. For example, to calculate the complementary angle of 72°, simply subtract it from 90°, i.e 90°- 72° = 18°. Below we have some more solved examples to clear your doubts.
Example
1. Find the value of angle X in the following right angle.
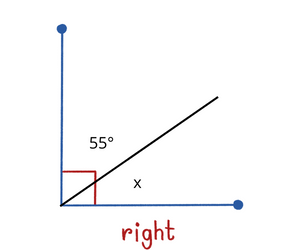
Solution :
From the figure, we can conclude that angles 55° and X° are complementary angles as the angle is right angle. We have to find the value of X.
Using the complementary angles formula,
Complementary Angles (X) = 90° – angle
Complementary Angles (X) = 90° – 55°
Complementary Angles (X) = 35°
The value of angle X is 35°.
Example
2. Find the complement angle of 31°
Solution :
Using the complementary angle formula,
Complementary Angle = 90° – angle
Complementary Angles = 90° – 31°
Complementary Angles = 59°
The complementary angle of 31° is 59°
Complementary Angles of 1° – 90°
The complementary angle of 1° to 90° is shown in the table below.
| Complementary Angle of | |
| 1° | 89° |
| 2° | 88° |
| 3° | 87° |
| 4° | 86° |
| 5° | 85° |
| 6° | 84° |
| 7° | 83° |
| 8° | 82° |
| 9° | 81° |
| 10° | 80° |
| 11° | 79° |
| 12° | 78° |
| 13° | 77° |
| 14° | 76° |
| 15° | 75° |
| 16° | 74° |
| 17° | 73° |
| 18° | 72° |
| 19° | 71° |
| 20° | 70° |
| 21° | 69° |
| 22° | 68° |
| 23° | 67° |
| 24° | 66° |
| 25° | 65° |
| 26° | 64° |
| 27° | 63° |
| 28° | 62° |
| 29° | 61° |
| 30° | 60° |
| 31° | 59° |
| 32° | 58° |
| 33° | 57° |
| 34° | 56° |
| 35° | 55° |
| 36° | 54° |
| 37° | 53° |
| 38° | 52° |
| 39° | 51° |
| 40° | 50° |
| 41° | 49° |
| 42° | 48° |
| 43° | 47° |
| 44° | 46° |
| 45° | 45° |
| Complementary Angle of | |
| 46° | 44° |
| 47° | 43° |
| 48° | 42° |
| 49° | 41° |
| 50° | 40° |
| 51° | 39° |
| 52° | 38° |
| 53° | 37° |
| 54° | 36° |
| 55° | 35° |
| 56° | 34° |
| 57° | 33° |
| 58° | 32° |
| 59° | 31° |
| 60° | 30° |
| 61° | 29° |
| 62° | 28° |
| 63° | 27° |
| 64° | 26° |
| 65° | 25° |
| 66° | 24° |
| 67° | 23° |
| 68° | 22° |
| 69° | 21° |
| 70° | 20° |
| 71° | 19° |
| 72° | 18° |
| 73° | 17° |
| 74° | 16° |
| 75° | 15° |
| 76° | 14° |
| 77° | 13° |
| 78° | 12° |
| 79° | 11° |
| 80° | 10° |
| 81° | 9° |
| 82° | 8° |
| 83° | 7° |
| 84° | 6° |
| 85° | 5° |
| 86° | 4° |
| 87° | 3° |
| 88° | 2° |
| 89° | 1° |
| 90° | 0° |