Have you ever considered finding the volume of the Egyptian Pyramids? You may use this square pyramid volume calculator to calculate the volume of a square pyramid.
<iframe src="https://calculatorhub.org/?cff-form=98" style="width:100%;height:100%;"></iframe>
A pyramid is a solid object with a base and edges traced from each vertex of the base that meet at a single point known as the pyramid’s apex. A pyramid’s base can be any polygon, but its other faces are invariably triangles.
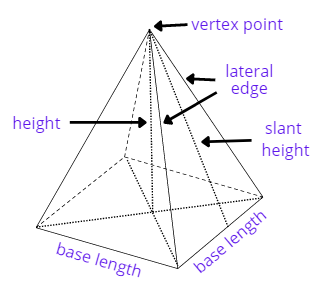
In the above square pyramid figure, ‘a’ represents the base length and ‘h’ represents the height of the square pyramid. Whereas ‘e’ and ‘H’ represents lateral edge and slant height respectively.
Volume of Square Pyramid Calculator Use
- It’s quite easy to use this square pyramid volume calculator.
- From the dropdown menu, select the known values of square pyramid.
- Simply input the known values of the square pyramid into the appropriate fields to calculate the volume.
- The calculator will calculate the volume of the square pyramid based on the entered value.
Square Pyramid Volume Formula
A simple formula can be used to find the volume of a square pyramid. Use the formula below to find the volume of a square pyramid.
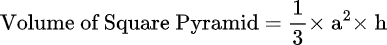
How to Find the Volume of Square Pyramid
Using the above mentioned pyramid volume formula, you could quickly calculate the volume of any square shaped pyramid object. The height and length of one side of the base are critical dimensions to know when calculating the volume of a square pyramid.
If you have these two values available, you can quickly calculate the volume. We have some solved examples below that will help you understand how to calculate the volume of a square pyramid.
Note : Make sure the measuring units (cm, ft, m, etc.) of the square pyramid height and the side length of the base are similar when applying the above volume formula.
Example
1. A ketchup bottle is shaped like a square pyramid with 5 inch sides and a 12 inch height. How much ketchup can the bottle hold, according to the square pyramid volume formula.
Solution :
Length of one side of the bottle base (a) = 5 in
Height of square pryamid-shaped bottle (h) = 12 in
Using the square pyramid volume formula,
Volume = 1/3 x a2 x h
Volume = 1/3 x 52 x 12
Volume = 99.99 in3
The volume of ketchup bottle is 99.99 cubic inches.
Find the Volume of a Square Pyramid Using Slant Height
You’ve learnt how to calculate the volume of a square pyramid using the height of the pyramid and the base length of one of its sides up to this point. But what if you don’t know the square pyramid’s height and are instead given the slant height?
This scenario appears to be difficult, but don’t worry, we’re always here to get you out of any mathematical problem.
You can use our square pyramid volume calculator to quickly calculate the volume. You may find the volume by directly inserting the slant height and base length values. But if you still want to calculate by hand, we give you a high five.
To calculate the volume, apply the formula above, but first determine the height of the pyramid. The pythagorean theorem is required for this. You can apply the standard formula above once you’ve determined the value of height.
Another formula exists solely to keep things simple. The formula below can be used to find the volume of a square pyramid directly using the slant height and base length value of one side.
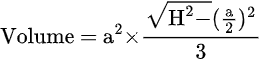
We’ve included a solved example below that demonstrates both techniques for calculating the volume of a square pyramid using the slant height and base length of one side.
Example
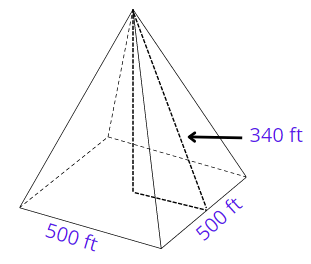
1. Square Pyramid in Egypt has a base measuring about 500 ft. × 500 ft. and the slant height of the pyramid is 340 ft. Find the volume of the square pyramid.
Solution :
Slant height of square pyramid (H) = 340 ft.
Base length of one side (a) = 500 ft.
First, we’ll try to calculate the volume using the easy way (second formula), which is to use the slant height and base length of one side directly into the formula.
Volume = a² * √(H² – (a / 2)²) / 3
Volume = 500² * √(340² – (500 / 2)²) / 3
Volume = 250000 * √(115600 – (250)²) / 3
Volume = 250000 * √(115600 – 62500) / 3
Volume = 250000 * √53100 / 3
Volume = 250000 * [(230.434372) / 3]
Volume = 250000 * 76.8114573
Volume = 19202864.3 ft3
We will now apply the second method, i.e the tricky method (first formula), to calculate the volume.
For this, you will first need to find the height of the pyramid by the Pythagorean theorem method (a2 + b2 = c2).
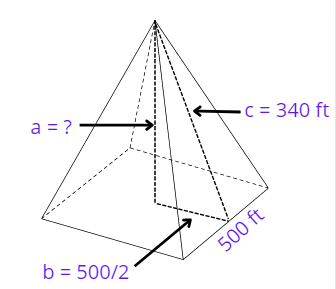
We have to consider the slant height of the pyramid as ‘c’, height of the pyramid as ‘a’ and half of the base length as ‘b’. You can see in the above figure that a right-angle has been formed.
c = 340 ft
b = 500/2 = 250 ft
a = ?
You can use our pythagorean theorem calculator directly to determine the missing value, or you can calculate it manually.
Using the Pythagorean theorem,
a2 + b2 = c2
a2 + 2502 = 3402
a2 + 62500 = 115600
a2 = 115600 – 62500
a2 = 53100
a = √53100
a (height) = 230.434372 ft
Note : Don’t confuse this (a = 230.434372) with the base length of one side. We have considered the height of the pyramid as ‘a’ to use it in the Pythagorean theorem. While using the value of ‘a’ in formula no 1, use the base length value of 500 ft.
The height (h) of the square pyramid is 230.434372 ft.
Now we can use the standard formula to find the volume of the square pyramid.
Volume = 1/3 x a2 x h
Volume = 1/3 x 5002 x 230.434372
Volume = 1/3 x 250000 x 230.434372
Volume = 19202864.3 ft3
You can cross check the final result obtained from both the methods. In our case, the values are the same. So you can use both the formulas to calculate the volume of a square pyramid using slant height and the base length of one side.
Find the Volume of Square Pyramid Using Lateral Edge
We’ve learnt how to determine the volume of a square pyramid using the height and base length, slant height and base length, and now we’ll learn how to find the volume of a square pyramid using the lateral edge length and the base length of one side.
The procedure of calculating volume is similar to that of determining volume using slant height. The formula is the only difference. You have two methods to find the volume here as well, exactly as we did in the above operation.
The formula for calculating the volume of a square pyramid directly using the lateral edge and one side’s base length is as follows:
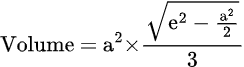
We have a solved example below that will show you how to find the volume step by step.
Example
1. Square Pyramid in Egypt has a base measuring about 550 ft. × 550 ft. and the lateral edge length of the pyramid is 480 ft. Find the volume of the square pyramid.
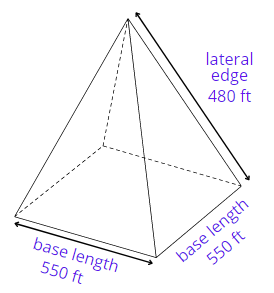
Solution :
Lateral edge length of square pyramid (e) = 480 ft.
Base length of one side (a) = 550 ft.
First, we’ll try to calculate the volume using the easy way (third formula), which is to use the lateral edge length and base length of one side directly into the formula.
Volume = a² * √(e² – (a²/ 2)) / 3
Volume = 550² * √(480² – (550²/ 2)) / 3
Volume = 302500 * √(230400 – (302500/2)) / 3
Volume = 302500 * √(230400 – 151250) / 3
Volume = 302500 * √(79150) / 3
Volume = 302500 * ((281.336098) / 3)
Volume = 302500 * 93.7786993
Volume = 28368056.5 ft3
We will now apply the second method, i.e the tricky method (first formula), to calculate the volume.
To do so, you must first determine the pyramid’s height. You don’t need to apply the Pythagorean theorem to compute the height of a square pyramid; instead, a simple formula can be used to calculate the height from the lateral edge and the base length.
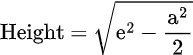
By using the above formula to calculate the height,
Height = √(e2 – (a2 /2))
Height = √(4802 – (5502 /2))
Height = √(230400 – 151250)
Height = √(79150)
Height (h) = 281.34 ft
Now we have the height of the square pyramid so we can directly use the standard formula (formula no 1) to calculate the volume,
Using the square pyramid volume formula,
Volume = 1/3 x a2 x h
Volume = 1/3 x 5502 x 281.336098
Volume = 0.33333333 x 302500 x 281.336098
Volume = 28368056.5 ft3
Find the Volume of Square Pyramid w/o Knowing the Base Length
You may also calculate the volume of a square pyramid without knowing the length of the base. However, you must know at least two values in this scenario, either height and slant height or lateral edge and slant height or height and lateral edge.
Using the formulas below, you can quickly calculate the volume if you know either of the two values.
1. Use this formula if you know the height (h) and slant height (H).
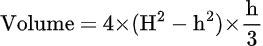
2. Use this formula if you know the lateral edge (e) and slant height (H).
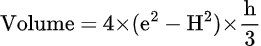
3. Use this formula if you know the height (h) and lateral edge (e).
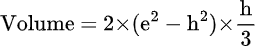
You can find the value of height (h) for any of the three formulas using the same approach we used before with the pythagorean theorem and formula no 4, whichever is relevant.